Gotowy na kolejny problem algorytmiczny do przeanalizowania 🧐? Dzisiaj przeanalizujemy sobie niejaki problem pokrycia zbioru - na czym on polega, jaką reprezentuje złożoność obliczeniową i na końcu, gotowe rozwiązanie w postaci działającego kodu źródłowego, od serca ❤️! Zainteresowany(-a) szczegółami 🙂? To zapraszam 😊!
NA CZYM POLEGA PROBLEM POKRYCIA ZBIORU?
Problem pokrycia zbioru (ang. set cover problem) dotyczy kwestii, przed którą stoi człowiek, który dysponując takimi elementami (literka 'U' oznacza "uniwersum" 💡) 👇:
U = {A, B, C, D, E}
posiada kilka różnych zbiorów, w których znajdują się poszczególne elementy:
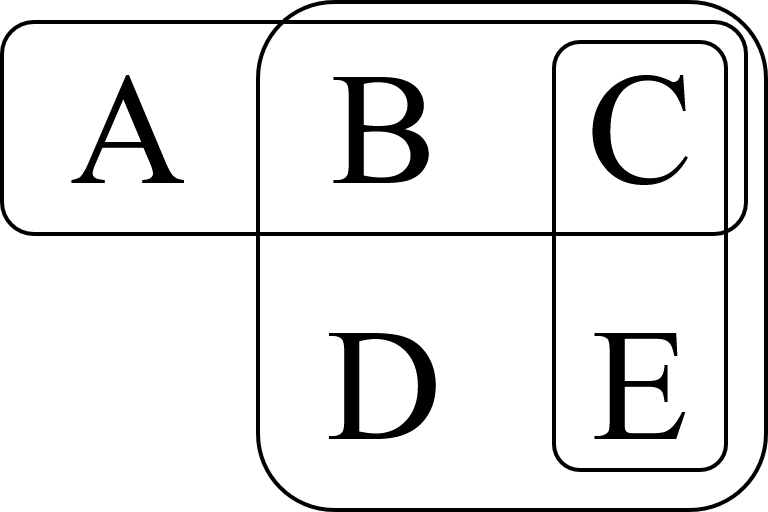 |
Rysunek prezentujący przynależność elementów do zbiorów na ukazanie problemu pokrycia zbioru.
a niektóre z nich znajdują się w więcej niż jednym zbiorze ⚠️. Sformułowanie może wyglądać następująco:
S = {{A, B, C}, {B, C, D, E}, {C, E}}
i zagadnieniem jest znaleźć taką minimalną liczbę zbiorów, aby uwzględnić wszystkie elementy podane w zbiorze U 🤔.
Problem: wyznaczenie takiego podzbioru zbiorów, aby ich suma zawierała wszystkie elementy zbioru U
Z ŻYCIA WZIĘTE
Jest od groma przykładów gdzie występuje problem pokrycia zbioru 👇:
- ustalenie które stacje telewizyjne mogą przynieść największą oglądalność przy zadanym budżecie,
- ustalenie w których częściach miasta najlepiej rozmieścić billboardy reklamowe, aby "wisiały" jak najdłużej i ściągnęły uwagę jak największej liczby osób, przy zadanym budżecie,
- ustalenie które witryny internetowe uwzględnić, aby wstawić na nich reklamę prowadzącą do naszej strony internetowej, przyciągając jak największą liczbę osób, przy zadanym budżecie.
Zauważ, że każdy z tych przykładów charakteryzuje się wyznaczeniem optymalnej "palety" możliwości. To są nasze zbiory z elementami 💡. Ponieważ zbiór, matematycznie, nie nadaje kontekstu, ustalamy go sami zależnie od sytuacji.
Stacja telewizyjna może mieć w sobie "element" w postaci przewidywanej liczby telewidzów 👨👩👧👦. Miasto, na którym znajdują się puste billboardy reklamowe mogą składać się "wartościowo" zarówno z liczby dostępnych miejsc, jak i liczby mieszkańców 🌎. A witryny internetowe, podobnie jak w telewizji, przewidywaną liczbę odwiedzających na dobę 📶.
Ponadto w każdym z nich napisałem o ograniczeniu w postaci posiadanego budżetu 💰. To już jest nieco bardziej rozbudowany problem, do którego dochodzi czynnik minimalizacji kosztów albo maksymalizacji zysków (albo jedno i drugie 😉), jednak my nie będziemy takiego rozpatrywać 🙂. Skupimy się tylko na kwestii wyznaczenia sumy zbiorów uwzględniającej wszystkie elementy, o które nam chodzi ✅.
Do dzieła 🔨! Rozpracujmy to ☺️!
ANALIZA PROBLEMU POKRYCIA ZBIORU
Ustalmy możliwe podejście zgodnie z rysunkiem u góry 👍. Mamy 3 zbiory do wyboru 3️⃣. Uwzględnienie lub nieuwzględnienie danego zbioru jest decyzją "zerojedynkową" (tak/nie). Zatem, mamy do zbadania 8 następujących kombinacji 👇:
| Lp | {A, B, C} | {B, C, D, E} | {C, E} |
| 1 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 |
| 3 | 0 | 1 | 0 |
| 4 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 |
| 6 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 |
| 8 | 1 | 1 | 1 |
Teraz wystarczy spośród tych opcji sięgnąć po tę, w której suma uwzględnionych podzbiorów daje nam wszystkie elementy (A-E), a tych podzbiorów jest jak najmniej ✅. To będzie nasze globalnie optymalne rozwiązanie 🏆.
Problem w tym, że liczba możliwych kombinacji będzie nam drastycznie rosła zależnie od liczby podzbiorów 😨! A problem pokrycia zbioru wymaga, aby "przetrząsnąć" każdy zbiór, każdy element i każdą kombinację celem wyznaczenia optymalnego rozwiązania (metoda "brute-force" 👊) ⚠️!
W związku z powyższym, uzyskujemy taką złożoność czasową w notacji dużego O (przypadek najgorszy):
O(2n)
2 podniesione do potęgi oznaczającej liczbę zbiorów 💥! To jest złożoność wykładnicza (jedna z najgorszych) 😱! To oznacza, że problem pokrycia zbioru, to problem NP-zupełny ❌!
Mamy podobną sytuację jak przy dyskretnym problemie plecakowym (opisanym w poprzednim materiale) 👜. Tym razem jednak, zamiast elementów mamy podzbiory i to one stanowią pojedynczy "element" (natomiast zbiór potęgowy wychodzi taki sam nieubłaganie) 😞.
WYMAGANE PODEJŚCIE APROKSYMACYJNE
Lipa 😅! Trzeba sobie radzić inaczej 🙂.
W tym miejscu pokażę Ci jedno z rozwiązań opierających się o zachłanność 🎯. Będzie to takie podejście, w którym dysponując tymi samymi zbiorami i elementami, "oblatujemy" zawartości wszystkich zbiorów i wyznaczamy "rekordzistę" pokrywającego największy fragment wymaganych elementów, których nie obejmują wcześniej wybrane zbiory 💥. Czynimy to tak długo, aż wszystkie elementy zostaną uwzględnione, zwracamy listę zbiorów i koniec 😁.
PROBLEM POKRYCIA ZBIORU "PO APROKSYMACYJNEMU"
Wyjaśniam jak działa algorytm aproksymacyjny do naszego problemu 📢! Na początku, notujemy sobie wszystkie elementy naszego uniwersum, które nas interesują 👇:
L = {A, B, C, D, E}
Następnie, zerkamy na dostępne zbiory z elementami 👀:
| Lp | Zbiór |
| 1 | {A, B, C} |
| 2 | {B, C, D, E} |
| 3 | {C, E} |
i wybieramy ten, który dysponuje największą liczbą tych elementów, których w dalszym ciągu nam brakuje 📈. Czyli bierzemy sobie zbiór nr 2 😊! Następnie, wykonujemy 2 czynności:
- "wycinamy" z naszej listy szukanych elementów te elementy, które znajdują się w wybranym przez nas zbiorze,
- notujemy nazwę wybranego zbioru i wstawiamy do listy "wybranych zbiorów".
Po takim zabiegu, nasza lista pozostałych szukanych elementów będzie wyglądać następująco:
L = {A}
Powtarzamy konsekwentnie te same kroki (od wybrania zbioru, do "ucinania" pozostałych elementów), aż lista szukanych elementów będzie pusta 0️⃣. Wtedy kończymy nasze poszukiwania i uzyskujemy rozwiązanie przybliżone ❤️!
Pamiętaj, że zachłanność polega na podejmowaniu decyzji przez algorytm na podstawie swojej obecnej wiedzy, zatem nie gwarantuje, że otrzymane rozwiązanie będzie "super" 🫵. Im większe zbiory danych do zbadania, tym bardziej narażamy się na odchylenie od rozwiązania dokładnego 😳. Natomiast nie mamy innego wyjścia i lepiej wziąć sobie rozwiązanie, które i tak będzie zadowalające, niż czekać nieakceptowalną ilość czasu na rozwiązanie dokładne dla ogromnych zbiorów danych 👍.
Takie podejście charakteryzować się będzie poniższą złożonością czasową (wg notacji dużego O):
O(|S|2)
Dosłowna "zamiana miejsc" algebraicznie 😄! Kwadrat z liczby zbiorów do zbadania 👍! Bo N razy poszukujemy zbiorów, które pokryją wszystkie poszukiwane elementy i za każdym razem musimy spośród wszystkich dostępnych wyznaczyć ten, który pokrywa największą pozostałą część - to "kosztuje" kolejne N razy 💱!
KOD ŹRÓDŁOWY
Przechodzimy do praktyki 🧨! Masz tu kod źródłowy w języku Java i popatrz sam(a) jak to wygląda, uruchamiając program ▶️!
KLASA "MAIN"
public class Main {
public static void main(String[] args) {
new Launcher();
}
}Tu jak zwykle mamy sam "zapalnik" w postaci instancji klasy uruchamiającej algorytm rozwiązujący problem pokrycia zbioru, więc to zostawiamy sobie na koniec 🙂.
REKORD "UNIVERSEELEMENT"
public record UniverseElement(String name) {
}To jest rekord dla pojedynczego elementu znajdującego się w naszym uniwersum (rekord w języku Java, to klasa danych z zestawem niemodyfikowalnych danych składowych ℹ️) 👍.
W naszym przykładzie, wystarczy żeby element składał się wyłącznie z łańcucha znaków jako nazwa (identyfikator) 🔤. Jeżeli jednak będziesz chciał(a) rozbudować sobie ten algorytm, aby wprowadzić dodatkowe cechy pojedynczego elementu np. liczbę mieszkańców na miasto albo przewidywaną liczbę obserwujących czyjegoś konta na Instagramie, to jest właściwe miejsce dla wprowadzenia tych danych 🔥!
KLASA "UNIVERSESET"
import java. util.stream.Stream;
import java. util.LinkedHashSet;
public class UniverseSet extends LinkedHashSet<UniverseElement> {
public UniverseSet(Stream<UniverseElement> elements) {
elements.forEach(this::add);
}
public UniverseSet() {}
}Po zdefiniowanym elemencie uniwersum, następny w kolejności jest pojedynczy zbiór elementów 👜.
Klasa dla zbioru elementów jest klasą potomną "LinkedHashSet", czyli kolekcji typu "zbiór" ("HashSet") zdolnej do zapamiętywania kolejności dodawanych elementów ("Linked") 🧠. Wewnątrz niej mamy tylko dwa konstruktory 👇:
- pierwszy akceptujący strumień elementów uniwersum (stworzony na celu wygodnego tworzenia zbiorów z możliwością dodawania elementów od razu, w momencie tworzenia obiektu),
- drugi bezparametrowy (stworzony na okoliczność utworzenia zbioru bez wstawiania elementów).
W konstruktorze przyjmującym strumień elementów, mamy jedyną instrukcję ("forEach"), za pomocą której wprowadzamy elementy ze strumienia do naszego zbioru ✅. I tyle, nic więcej nie trzeba tłumaczyć 😄!
KLASA "UNIVERSE"
import java. util.Arrays;
import java. util.LinkedHashSet;
public class Universe {
private final LinkedHashSet<UniverseSet> sets = new LinkedHashSet<>();
private final LinkedHashSet<UniverseElement> elements = new LinkedHashSet<>();
public Universe() {
createNewElements("A", "B", "C", "D", "E");
createNewSet("A", "B", "C");
createNewSet("B", "C", "D", "E");
createNewSet("C", "E");
}
public LinkedHashSet<UniverseSet> getSets() {
return sets;
}
public LinkedHashSet<UniverseElement> getElements() {
return elements;
}
private void createNewElements(String... namesOfElementsToAdd) {
var listOfNamesOfElementsToAdd = Arrays.asList(namesOfElementsToAdd);
listOfNamesOfElementsToAdd.forEach(elementName -> elements.add(new UniverseElement(elementName)));
}
private void createNewSet(String... namesOfElementsToAdd) {
var listOfNamesOfElementsToAdd = Arrays.asList(namesOfElementsToAdd);
var streamOfElementsWithGivenNames = elements.stream().filter(element -> listOfNamesOfElementsToAdd.contains(element.name()));
var setInstance = new UniverseSet(streamOfElementsWithGivenNames);
sets.add(setInstance);
}
}A tu mamy w końcu nasze całe uniwersum 🌎! Klasa robiąca nam za "sumę" wszystkich pojedynczych elementów i wszystkich zbiorów elementów.
U góry mamy dwie składowe finalne ("finalne" oznacza, że raz przypisanej referencji, nie można zmienić) 👇:
- zbiór zbiorów elementów (masełko maślane 🙃),
- zbiór pojedynczych elementów.
Wydzieliłem to w taki sposób, aby w kodzie dać możliwość swobodnego tworzenia zbiorów poprzez podanie samych nazw tych elementów, które chcemy do niego wprowadzić 💖.
Konstruktor składa się z serii wywołań metod:
- najpierw jest tworzenie samych instancji elementów (poprzez podanie samych nazw),
- potem odbywa się tworzenie zbiorów elementów (również poprzez podanie samych nazw).
Kolejne dwie metody służą jedynie do pobierania zbiorów i samych elementów (to jest potrzebne w samym procesie algorytmicznym, do którego niebawem przejdziemy ℹ️).
Metoda tworząca elementy po samych nazwach korzysta ze zmiennej liczby argumentów 😲. To też ma na celu podniesienie wygody korzystania z niej, aby nie trzeba było otaczać wielu argumentów wywołaniem "Arrays.asList", które potrafi być upierdliwe w tym języku 😜. Tę "otoczkę" robimy sobie już w środku metody, a następnie, poprzez "forEach", tworzymy sobie instancje obiektów 📦.
W przypadku, gdybyś miał(a) więcej danych do wstawienia na element, to niestety czeka Cię obróbka tej metody, tak aby móc przekazać resztę niezbędnych wartości stanowiących daną elementu (tak jak teraz jest nią nazwa) ⚠️.
Tworzenie pojedynczego zbioru również korzysta ze zmiennej liczby parametrów i tutaj także jest "otoczenie" metodą "pakującą" podane nazwy w listę, natomiast samo "wnętrze" instrukcji wygląda już inaczej 🙂. Korzystamy z podejścia funkcyjnego, dokładnie w tym miejscu:
var streamOfElementsWithGivenNames = elements.stream().filter(element -> listOfNamesOfElementsToAdd.contains(element.name()));Ta linijka oznacza: "skonwertuj zbiór na strumień i wyklucz te elementy, których nazwy nie znajdują się w podanej przez Ciebie liście" 💪. To nam wystarczy do przefiltrowania elementów w taki sposób, aby zostały tylko te, które chcemy umieścić ✔️.
Niżej mamy utworzenie nowego zbioru (konstruktor, do którego wstawiamy nasz otrzymany strumień 😉) i dodanie go do zbioru zbiorów 😅!
Czy dostrzegasz słówko "var" w kodzie 😄? W języku Java, jest to wygodny skrót do pominięcia wstawiania typu danych zmiennej lokalnej i "zrzucenia" tego ciężaru na kompilator 😁!
KLASA "RESULTSPRINTER"
import java. io.PrintStream;
import java. util.Set;
public class ResultsPrinter {
private final PrintStream printStream = System.out;
public <T> void printAboutSet(Set<T> set, String message) {
printStream.println(message + set);
}
}Ta klasa służy nam jedynie do wypisywania komunikatów podczas działania algorytmu rozwiązującego problem pokrycia zbioru ℹ️. W jej środku mamy tylko jedną metodę służącą właśnie wypisywaniu komunikatu na temat zbioru 💬.
Aby uczynić tę metodę reużywalną, wstawiłem typ generyczny, tak aby można było bez problemu skorzystać z niej wstawiając zbior z elementami dowolnego typu (nie tylko naszych elementów uniwersum) 🎉!
KLASA "LAUNCHER"
import java. util.HashSet;
import java. util.Comparator;
public class Launcher {
private final Universe universe = new Universe();
private final HashSet<UniverseSet> chosenSetsOfElements = new HashSet<>();
private final HashSet<UniverseElement> leftElementsFromUniverse = new HashSet<>(universe.getElements());
private final ResultsPrinter resultsPrinter = new ResultsPrinter();
public Launcher() {
while (!leftElementsFromUniverse.isEmpty()) {
findNextMostCoveringSet();
}
resultsPrinter.printAboutSet(chosenSetsOfElements, "Wybrane zbiory pokrywające wszystkie elementy: ");
}
private void findNextMostCoveringSet() {
var mostCoveringSetOfElements = getMostCoveringSetOfElements();
leftElementsFromUniverse.removeAll(mostCoveringSetOfElements);
chosenSetsOfElements.add(mostCoveringSetOfElements);
resultsPrinter.printAboutSet(mostCoveringSetOfElements, "Wybrany zbiór z największą liczbą szukanych elementów: ");
}
private UniverseSet getMostCoveringSetOfElements() {
var universeSets = universe.getSets();
var optionalUniverseSetWithHighestNumberOfLeftElements = universeSets.stream().max(Comparator.comparingLong(set -> set.stream().filter(leftElementsFromUniverse::contains).count()));
return optionalUniverseSetWithHighestNumberOfLeftElements.orElseGet(UniverseSet::new);
}
}Tak doszliśmy do ostatniej klasy, w której następuje "odpalenie" algorytmu 🔥. U góry mamy 4 (finalne) składowe 👇:
- obiekt całego uniwersum,
- obiekt zbioru przechowujące wszystkie "wybrane" przez nas zbiory,
- obiekt zbioru przechowującego wciąż poszukiwane elementy,
- obiekt do wypisywania komunikatów.
W konstruktorze mamy pętlę "while", która odpowiada za miejsce powtarzania kroku "wycinania" elementów poszukiwanych 🆕. Dopóki nie odnajdziemy wszystkich elementów, o które nam chodzi, dopóty kontynuujemy poszukiwania 🔍. Określając to matematycznie, powtarzamy czynności dopóki suma wszystkich wyznaczonych zbiorów nie będzie równa naszemu uniwersum 💡:
A ∪ B = {A, B, C, D, E} = U
Na samym końcu tej samej metody mamy wypisanie końcowego wyniku w postaci wszystkich uwzględnionych zbiorów (które odbywa się po zakończeniu iterowania w pętli 🙂).
"Powtarzalny" krok znajduje się w osobnej metodzie (następnej w kolejności idąc od góry do dołu) ▶️. Najpierw tworzymy sobie zmienną do przechowywania zbioru pokrywającego największą liczbę dotąd nieodnalezionych elementów (zbiór ten wyznaczany jest w ostatniej metodzie w tej klasie ℹ️). Potem, wykonujemy 3 kroki:
- skreślamy ze zbioru poszukiwanych te elementy, które znajdują się w wyznaczonym zbiorze,
- dodajemy ten sam zbiór do zbioru zbiorów (do "rejestrowania" które uwzględniliśmy) 🙃,
- wypisujemy komunikat na temat wyznaczonego zbioru.
No i ostatnia metoda do wyjaśnienia 🎯! W celu wyznaczenia zbioru pokrywającego największą liczbę poszukiwanych elementów, pobieramy sobie w pierwszym kroku wszystkie zbioru jakie znajdują się w uniwersum 🌐. Następnie, ponownie korzystamy ze strumieni i poniższej instrukcji:
var optionalUniverseSetWithHighestNumberOfLeftElements = universeSets.stream().max(Comparator.comparingLong(set -> set.stream().filter(leftElementsFromUniverse::contains).count()));która, w przetłumaczeniu na język polski 🇵🇱, oznacza: "skonwertuj zbiory na strumień, wyznacz ten, który posiada największą liczbę elementów pokrywających się ze zbiorem pozostałych elementów jakie szukamy i zwróć ich liczbę" 😱.
"Comparator.comparingLong" to wbudowany budulec do porównywania ze sobą zbiorów pod kątem liczby elementów spełniających podane kryterium (którym w tym przypadku, jest zbadanie czy element znajduje się w zbiorze poszukiwanych 🔎) 🚀. Wyjaśniłem w osobnym artykule do czego w języku Java służy komparator 📖.
Warto zwrócić uwagę w tym miejscu, że typ tej zmiennej to jest "Optional" 💥. "Optional" w języku Java stanowi "otoczkę" wokół typu referencyjnego, które jak możesz wiedzieć, jest zagrożone brakiem referencji (wartość "null") ⚠️. "Optional" skutecznie "chroni" nas przed zgłaszaniem wyjątków przez program w momencie próby powołania się na dowolną składową obiektu, który przyjmuje wartość "null" ℹ️.
Z tego względu, instrukcja "return" może na starcie budzić zdziwienie. Natomiast nie ma się czego bać 😄! To:
return optionalUniverseSetWithHighestNumberOfLeftElements.orElseGet(UniverseSet::new);oznacza w skrócie: "zwróć na wyjściu znalezioną referencję do zbioru o największej liczbie poszukiwanych elementów, a w przypadku wartości >>null<<, zwróć nowy pusty zbiór" 🌟. Teraz już wiesz po co był tamten pusty konstruktor 😊!
Na tym kończymy tłumaczenie całego kodu 🏁!
Gotowe! Pokazane, wytłumaczone i rozwiązane na własnym przykładzie. Banalnym 🍌, jeśli chodzi o ścisłość 😁. Problem pokrycia zbioru uznaję za temat zamknięty 🔒!
