Zaczynamy kolejny temat z algorytmiki 🧨! W tym artykule dowiesz o kolejnym algorytmie sortującym: sortowanie szybkie ⚡! Tradycyjnie wyjaśniam zasadę działania, złożoność czasową i na deser, kod źródłowy ❤️! Zapraszam do środka 😉!
SORTOWANIE SZYBKIE. TYLKO, NA JAKIEJ PODSTAWIE "SZYBKIE"?
Można sobie myśleć: "a co, w takim razie reszta algorytmów jest wolna, czy co?!" 😄. To nie chodzi o nazwę, tylko o sposób działania 😉.
Sortowanie szybkie (ang. quicksort) to algorytm sortujący elementy w danym zbiorze (wprowadzonym w ramach danych wejściowych) charakteryzujący się niziutką złożonością obliczeniową 😱! Nazwa pochodzi od faktycznie szybkiego i efektywnego wyznaczania rozwiązania, w porównaniu do innych znanych podejść algorytmicznych 🚀. Aczkolwiek musisz wiedzieć, że w przypadku sortowania szybkiego, jest to pojęcie względne ⚠️!
Przeanalizujmy sposób działania 🔍! Potem wyjaśnię wszystkie szczegóły 👍.
Problem: uporządkowanie zbioru elementów w kolejności rosnącej/malejącej według ustalonego kryterium (znowu 🙂)
SZYBKOŚĆ TKWI...W DZIELENIU
Sortowanie szybkie charakteryzuje się "przecinaniem" otrzymanego zbioru danych na 2 równe części wykorzystując tzw. "punkt osiowy" (ang. pivot), czyli element o wartości pomiędzy tymi o najmniejszej wartości, a tymi o największej. Punkt osiowy jest wyznaczany przez nas i w dalszej części dowiesz się jak duże odgrywa znaczenie w złożoności obliczeniowej ⚠️!
Następnie, opierając się na metodyce "dziel i zwyciężaj", konsekwentnie dzieli części danych na jeszcze mniejsze (przypadek rekurencyjny 🔁), aż do otrzymania jednego z 3 wyników (przypadek podstawowy 1️⃣) 👇:
- część posiada 2 elementy,
- część posiada tylko jeden element,
- część nie posiada żadnych elementów.
Powodem sprowadzania części do takich postaci jest trywialność w rozstrzygnięciu kolejności elementów 🧩. Jeżeli nie ma żadnych elementów lub jest tylko jeden element, to nie ma czego sortować i ma po prostu zwrócić listę taką, jaka jest 😁! Jeżeli są 2, to wystarczy sprawdzić czy jeden element ma większą wartość od drugiego i w przypadku prawdy, zamienić miejscami i zwrócić 👍!
Algorytm, gdy natrafi na powyższe przypadki, zaczyna "sklejać" ze sobą części otrzymanych list powracając do początku stosu wywołań, aż dojdzie do złączenia ze sobą dwóch posortowanych już połówek, tym samym kończąc wyznaczanie rozwiązania 💪!
EFEKTYWNOŚĆ ZALEŻNA OD PUNKTU OSIOWEGO
Teraz czas odpowiedzieć sobie na pytanie jaka jest złożoność obliczeniowa tego algorytmu ⌚! No właśnie. To zależy 🤨!
Aby zagwarantować optymalne dzielenie zbioru danych na połowy, trzeba dobrać taki punkt osiowy, który zawsze będzie dzielił dane na 2 równe części ✂️! W tym przypadku to będzie mediana 💡. To jest najbardziej pożądana sytuacja ✅.
Najgorzej, gdybyśmy dobierali punkt osiowy zawsze z brzegu (pierwszy lub ostatni element), ponieważ stos wywołań będzie niepotrzebnie rósł z powodu braku "równowagi" pomiędzy otrzymywanymi połówkami danych ❌!
Z tego powodu, złożoność czasowa sortowania szybkiego zależy od Ciebie i od Twojego dobierania punktu osiowego 🫵!
Jeżeli założymy, że punkt osiowy będzie zawsze dobierany optymalnie (najbardziej pasujący element w postaci mediany), to mamy wtedy taką złożoność 👇:
O(log(n))
Logarytm z liczby elementów przy podstawie 2 💥! Jest to bardzo pozytywny wynik zapewniający nieznaczny wzrost liczby iteracji względem danych wejściowych ☑️. To jest przypadek optymistyczny 🌞.
Przypadek średni (sytuacja, w której dobieramy właściwy punkt osiowy "na ogół"), przyniesie nieco gorszy rezultat w postaci takiej złożoności:
O(n*log(n))
Iloczyn liczby elementów i logarytmu z liczby elementów przy podstawie 2 💣.
Z kolei kiepskie dobieranie punktu osiowego (zawsze z lewej bądź prawej granicy), spowoduje otrzymanie takiej złożoności:
O(n2)
Kwadrat z liczby elementów 💀! Żeby zrozumieć dlaczego tak się dzieje, musisz sobie wyobrazić stos wywołań i jego "wzrost" co każde dzielenie listy na mniejsze części.
DZIAŁANIE "REDUKCJI POZIOMU" PROBLEMU
Sortowanie szybkie korzysta z metodyki "dziel i zwyciężaj", a więc "dzieli problem" na mniejsze podproblemy. Przypomnę w tym miejscu, że rekurencja tworzy "pod maską" stos wywołań tej samej funkcji ℹ️. Za każdym razem, gdy musimy podzielić zbiór danych na mniejsze kawałeczki aż do doprowadzenia do dwóch lub mniej elementów, kosztuje to dodatkowy cykl 💸. Im większa głębokość stosu, tym większa złożoność i więcej pracy dla procesora 🥵.
Jeżeli założymy, że za każdym razem jest optymistycznie i punkt osiowy jest wybrany jako optymalny, to za każdym razem dzielimy dane na 2 równe części - na lewo idą mniejsze od punktu osiowego, a na prawo, większe ✅. Czyli będziemy mieli taki "spadek" 👇:
{n / 2, n / 4, n / 8, ...}
A jeżeli punkt osiowy będzie za każdym razem dobierany źle ❌, czyli po lewej stronie będzie pusty zbiór danych, a po prawej taki sam z liczbą elementów obniżoną o 1, to głębokość stosu wywołań przyjmie taką formę:
{n - 1, n - 2, n - 3, ...}
Czyli zwróć uwagę, że wtedy mamy taką samą postać, jak przy sortowaniu przez wybieranie 😱! Idziemy element po elemencie 🚶.
Stąd, aby zmniejszyć liczbę cykli rekurencyjnych, musimy zmniejszyć stos wywołań 🔥! A możemy to zrobić jedynie poprzez wybranie takiego punktu osiowego, aby podzielone zbiory miały elementy rozłożone w miarę równomiernie 💡. Dlatego tak ważne jest, aby dobierać optymalny punkt osiowy, który pozwoli na podzielenie danych na 2 równe części 💎!
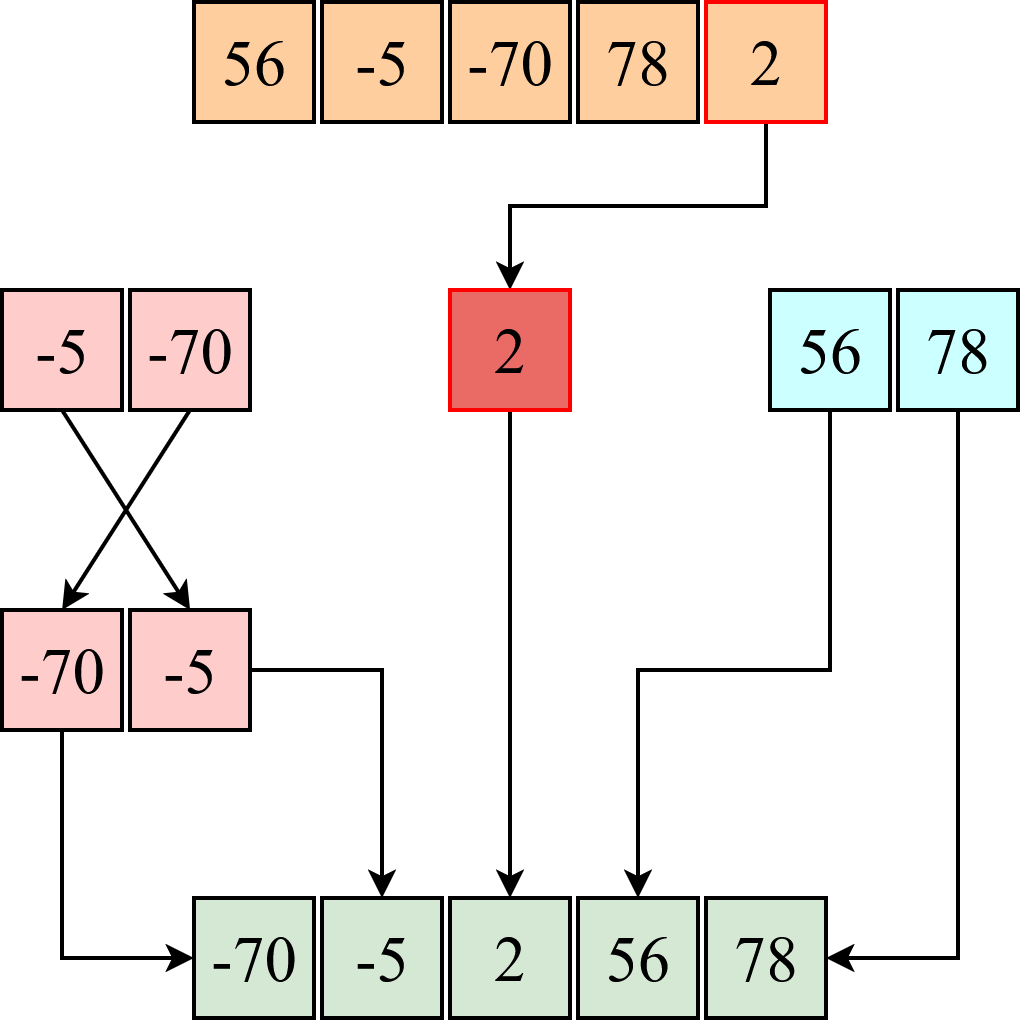 |
"Quicksort" czyli sortowanie szybkie, polega na konsekwentnym dzieleniu zbioru danych na mniejsze części, aż ustalenie kolejności stanie się trywialne (rozmiar podzbioru <= 2), a następnie łączeniu wszystkich podzbiorów w całość.
SPOSOBY WYZNACZANIA PUNKTU OSIOWEGO
Powiedzieliśmy sobie, żeby najlepiej dobierać punkt osiowy jako medianę. OK, tylko co - mamy za każdym razem ją wyznaczać 😕? Przecież wymaga ona posortowanych danych 😞! Także, co możemy zrobić 🤔?
Mamy 3 opcje uznane za dobre kompromisy, jeśli chodzi o wyznaczenie dobrego punktu osiowego w sortowaniu szybkim 👇:
- wybór pseudolosowy,
- wybór środkowego elementu,
- wyznaczenie mediany z trzech liczb (ang. "median-of-three").
WYBÓR PSEUDOLOSOWY
Możemy wybierać punkt...pseudolosowo 😊! Co prawda jesteśmy narażeni na dobranie złej wartości, aczkolwiek mamy też szansę trafić na medianę bądź wartość bliską medianie, co statystycznie i tak daje nam o wiele lepszą sytuację, niż wybranie wartości z lewego bądź prawego końca 😝. Wylosowanie takiego punktu "na pałę" daje dostatecznie dobre rezultaty - minimalizujemy szansę na otrzymanie kwadratowej złożoności obliczeniowej 📉.
WYBÓR ŚRODKOWEGO ELEMENTU
Wybranie od razu środkowego elementu ze zbioru też jest już o wiele lepszym pomysłem, niż wzięcie z lewej bądź z prawej strony. Wtedy dochodzi do pewnego podzielenia zbioru na 2 równe części, dlatego to jest dobre podejście 👍!
WYZNACZENIE MEDIANY Z TRZECH LICZB
Ostatnią znaną metodą, jest mediana z trzech liczb 3️⃣. W danej iteracji pobierasz pierwszy, środkowy i ostatni element w zbiorze danych. Potem poprzez posortowanie ich w kolejności rosnącej (albo zdefiniowane instrukcje warunkowe), pobierasz środkową wartość (medianę), która staje się punktem osiowym 🎯.
KOD ŹRÓDŁOWY
A teraz czas na kod źródłowy w Javie ukazujący sortowanie szybkie w akcji (do wyznaczania punktów osiowych, korzystam z pseudolosowości) 🎬!
KLASA "MAIN"
public class Main {
public static void main(String[] args) {
new Launcher();
}
}Standardowo wszystko zaczyna się od tej klasy, która uruchamia nasz algorytm ▶️.
KLASA "NUMBERSLIST"
import java. util.Random;
import java. util.ArrayList;
import java. util.stream.Collectors;
import java. util.function.Predicate;
public class NumbersList extends ArrayList<Integer> {
private static final Random random = new Random();
public NumbersList(int ...numbers) {
for (var number : numbers) {
add(number);
}
}
public int getRandomNumber() {
var numberOfElements = size();
if(numberOfElements == 0) {
return Integer.MIN_VALUE;
}
var randomIndex = random.nextInt(0, numberOfElements);
return get(randomIndex);
}
public NumbersList getNumbersWithMetCondition(Predicate<Integer> condition) {
return stream().filter(condition).collect(Collectors.toCollection(NumbersList::new));
}
}Tu mamy klasę potomną od "ArrayList" z zestawem metod pomocniczych związanych z procesem sortowania ℹ️. Posiada dodatkowo składową finalną typu "Random", która pozwala na sięgnięcie do metod pseudolosujących 🎲. Jest ona statyczna, ponieważ nie ma potrzeby tworzyć maszyny losującej co każdą kopię typu tej klasy 👍.
W konstruktorze wstawiłem za parametr zmienną liczbę parametrów, która pozwala wygodnie wstawiać liczby bez "opakowywania" w wywołanie "Arrays.asList" ❤️. W środku metody jest pętla rozszerzona, za pomocą której dodajemy sobie liczby jedna po drugiej ✅.
Niżej mamy metodę do losowania liczby z listy 🔀. Najpierw sprawdzamy czy liczba elementów pozwala w ogóle na wylosowanie czegokolwiek 🔍. Jeżeli nie, to zwracamy najmniejszą wartość jaką może przechowywać typ całkowitoliczbowy (-231). W przeciwnym wypadku, losujemy sobie indeks przy pomocy metody "nextInt". Zakres wyznaczamy zgodnie z notacją indeksową, aczkolwiek metoda nie uwzględnia górnej granicy, więc nie musimy pomniejszać o jeden (nawias okrągły domykania przedziału w matematyce) ⚠️. Następnie zwracamy wartość elementu pod wylosowanym indeksem, używając metody "get". Na tym metoda się kończy 🏁.
Metoda na samym dole korzysta z podejścia funkcyjnego 😮. Mianowicie, na podstawie zdefiniowanego predykatu (kryterium spełnialności), filtrujemy sobie zbiór liczb i w ten sposób możemy wyznaczać taką różnicę zbiorów, czyli wykluczamy elementy, które nie spełniają podanego warunku 🌟. Korzystamy tutaj z wielu osobnych kroków, które złączone w całość, zwracają nam listę liczb, które spełniają zadany warunek ☑️. Kroki są następujące 👇:
- konwersja kolekcji na strumień ("stream"),
- przefiltrowanie kolekcji na bazie podanego warunku ("filter"),
- "przepakowanie" danych ze strumienia do nowej instancji kolekcji ("collect"),
- utworzenie nowej instancji kolekcji na bazie "zbieracza" ("Collectors.toCollection").
Jednym zdaniem, cała ta instrukcja:
return stream().filter(condition).collect(Collectors.toCollection(NumbersList::new));oznacza: "przejrzyj wszystkie elementy w liście, wyklucz te, które nie spełniają zadanego warunku, zbierz przefiltrowane elementy i wstaw je do nowo utworzonej listy" 📖.
Z innej beczki - słowo "var" w języku Java, pozwala Tobie uniknąć wpisywania jawnie typu danych w miejsce tworzenia zmiennych lokalnych 🔥.
KLASA "RESULTSPRINTER"
import java. io.PrintStream;
import java. util.ArrayList;
public class ResultsPrinter {
private final PrintStream printStream = System.out;
public void printIntegerList(ArrayList<Integer> numbers, String message) {
printStream.println(message + numbers);
}
}To jest klasa pomocnicza do wypisywania komunikatu w ekranie terminala 💻. Nie należy do części sortowania szybkiego, więc jak najbardziej możesz ją usunąć, gdy nie potrzebujesz informacji w konsoli 😊.
Metoda jaką wprowadziłem, służy do wypisywania podanego komunikatu z użyciem listy liczb całkowitych, także po wstawionym dowolnym łańcuchu znaków, ujrzysz zaraz po nim liczby jakie się znajdują w podanej liście 😊.
KLASA "LAUNCHER"
import java. util.*;
public class Launcher {
private final NumbersList unsortedNumbers = new NumbersList(56, -5, -70, 78, 2);
private final ResultsPrinter resultsPrinter = new ResultsPrinter();
public Launcher() {
resultsPrinter.printIntegerList(getSortedNumbers(unsortedNumbers), "Posortowane liczby: ");
}
private ArrayList<Integer> getCombinedSortedNumbers(NumbersList numbersBelowPivot, int pivot, NumbersList numbersAbovePivot) {
var sortedNumbersBelowPivot = getSortedNumbers(numbersBelowPivot);
var sortedNumbersAbovePivot = getSortedNumbers(numbersAbovePivot);
var combinedSortedNumbers = new ArrayList<>(sortedNumbersBelowPivot);
combinedSortedNumbers.add(pivot);
combinedSortedNumbers.addAll(sortedNumbersAbovePivot);
return combinedSortedNumbers;
}
private ArrayList<Integer> getSortedNumbers(NumbersList numbers) {
if(numbers.size() <= 1) {
return numbers;
} else if(numbers.size() == 2) {
return getSortedPairOfNumbers(numbers);
} else {
var pivot = numbers.getRandomNumber();
var numbersBelowPivot = numbers.getNumbersWithMetCondition(number -> number < pivot);
var numbersAbovePivot = numbers.getNumbersWithMetCondition(number -> number > pivot);
return getCombinedSortedNumbers(numbersBelowPivot, pivot, numbersAbovePivot);
}
}
private ArrayList<Integer> getSortedPairOfNumbers(ArrayList<Integer> numbers) {
if(numbers.get(1) < numbers.get(0)) {
Collections.swap(numbers, 0, 1);
}
return numbers;
}
}Tu znajduje się sortowanie szybkie ⚡! Ze względu na swoje działanie i budowę rekurencji w kodzie, zrobiło się nieco więcej wierszy w jednej klasie. Idźmy jak zwykle od samej góry 🗻!
Klasa ma 2 finalne składowe 👇:
- listę nieposortowanych liczb,
- obiekt do wypisywania komunikatów (część poza algorytmem, którą można usunąć).
Konstruktor klasy składa się tylko z jednego wywołania metody: wypisywania komunikatu o posortowanych danych wejściowych ℹ️. Natomiast pierwszy parametr zawiera wywołanie metody, która jest punktem startowym sortowania szybkiego:
getSortedNumbers(unsortedNumbers)Tłumaczę co się dzieje od momentu wejścia do niej 🚩!
PRZYPADKI PODSTAWOWE
Tak jak opisałem wyżej, sortowanie szybkie "kroi" dane na coraz mniejsze części, aż do sprowadzenia do prostych do rozstrzygnięcia następujących problemów:
- otrzymanie zbioru z jedną liczbą,
- otrzymanie zbioru z dwiema liczbami.
Instrukcje warunkowe w pełni odpowiadają podanym opcjom 👍. Jeżeli zbiór zawiera nie więcej niż jeden element, natychmiast go zwracamy - to jest koniec podproblemu i "powracanie" do początku stosu ✔️. Jeżeli posiada dokładnie 2 elementy, to także mamy prostą sprawę bowiem wystarczy sprawdzić czy układają się w kolejności rosnącej, zamienić je miejscami w razie potrzeby i zwrócić zbior - to również oznacza koniec podproblemu i "powracanie" do początku 😊. Za to odpowiada metoda umieszczona na samym dole.
Do zamiany elementów miejscami, możesz użyć statycznej metody "swap" z klasy "Collections":
Collections.swap(numbers, 0, 1);A teraz...trzeci przypadek 😱!
PRZYPADEK REKURENCYJNY
Kiedy zbiór ma więcej niż 2 elementy, to musimy go podzielić na mniejsze części 🧩.
Najpierw wyznaczamy sobie punkt osiowy używając wyjaśnionej wcześniej metody do pobierania losowego elementu 🎲. Następnie, dzielimy zbiór danych na 2 podzbiory 👇:
- liczby mniejsze od punktu osiowego,
- liczby większe od punktu osiowego.
W obu przypadkach posługuję się wygodną metodą akceptującą predykat, dzięki któremu mogę przekazać inny warunek jaki element musi spełniać, aby występował w przefiltrowanym zbiorze 👀.
Po uzyskaniu punktu osiowego, zbioru z liczbami mniejszymi od punktu osiowego oraz zbioru z liczbami większymi od punktu osiowego, wywołujemy odrębną metodę "sklejającą" wszystkie części w jedną całość (to jest ta zaraz pod konstruktorem) ✊!
Oto co się w niej dzieje:
- wyznacza posortowaną lewą część zbiorów,
- wyznacza posortowaną prawą część zbiorów,
- tworzy nowy zbiór,
- dodaje do nowego zbioru posortowaną lewą część zbiorów,
- dodaje punkt osiowy (który będzie elementem środkowym),
- dodaje do nowego zbioru posortowaną prawą część zbiorów,
- zwraca pełny posortowany zbiór.
Czyli jak widzisz, metoda wyznacza zbiory i konsekwentnie je "skleja", aż do otrzymania kompletu posortowanych danych 🎁! To kończy działanie algorytmu i zarazem całego programu 🏁!
Java nie zezwala na tworzenie list wprowadzając jednocześnie inne listy i pojedyncze dane ⛔, stąd musiałem podzielić na instrukcje tak, a nie inaczej 🤷♂️. Mogą one nie odzwierciedlać zasady działania opisanej teoretycznie, natomiast Java nie posiada takich abstrakcyjnych zapisów jakie znaleźlibyśmy choćby w Pythonie typu: "zwróć [lewy podzbiór] + [punkt osiowy] + [prawy podzbiór]". Jeżeli jednak przyjrzysz się działaniu, to zobaczysz, że kod w całości odpowiada temu, co napisałem na samym początku ✔️.
Zakończyliśmy wspólnie wątek sortowania szybkiego 😊. Może wymagać kilkunastogodzinnych posiedzeń przy wyświetlaczu 📺, jednak gdy raz wpadnie do głowy zrozumienie, to już Ci tam zostanie i od tej pory będziesz wiedzieć jak działa "qsort" w języku C 😉!
